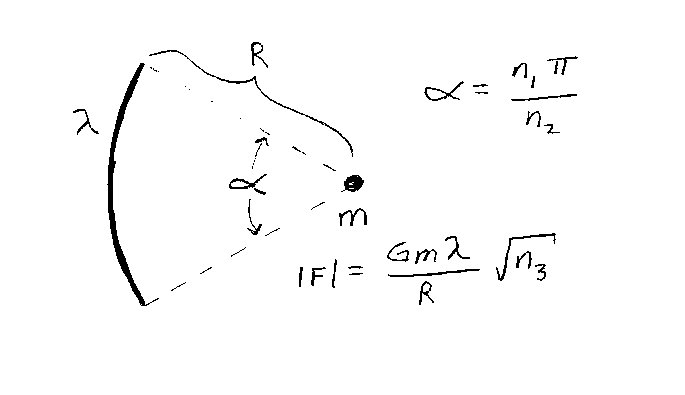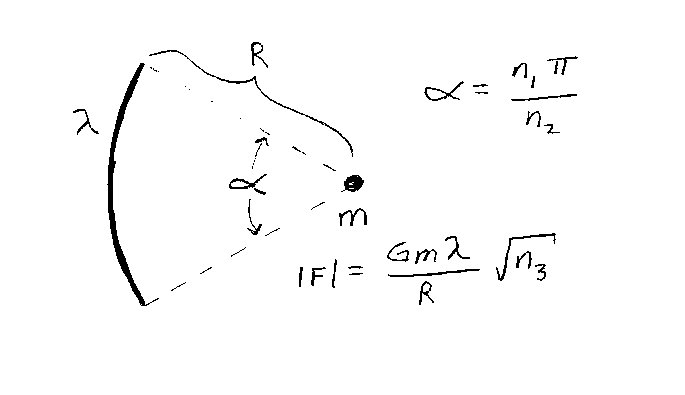Problem B9: Consider the two objects below. One is very small (point object) with mass m, and the other is a very thin circular arc of radius R whose mass is uniformly distributed. The object of mass m is located at the center of the circle of the arc. The linear density, mass per unit length, of the arc is λ. The full angle that the arc subtends is α=(n₁/n₂)π. Find the magnitude of the net force on the object of mass m. If the magnitude of the net force on the object equals F=(Gmλ/R) √ n₃, what is n₃? Note that all the integers are unitless,

n1 =	n2 =	Input n3:

If you are currently in my class, you can record your grade by entering your name and student ID number (without the leading zeros) below and clicking on "record grade".

First Name =	Last Name =	ID =
Problem: