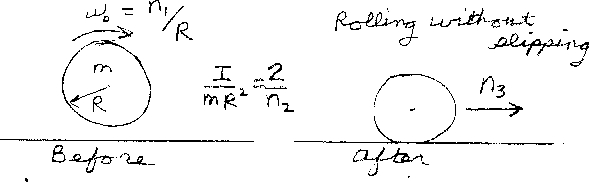
Problem D8:
A circular object of mass m and radius R starts out spinning in the air just above the floor. While
spinning with an initial angular velocity of ω0 = n1/R,
it is gently placed on the floor. There is friction between the object and the
floor causing it to move to the right while the angular velocity decreases.
Finally, the object rolls without slipping attaining a final speed of
n3. If the rotational inertia I divided by mR2 of the
object equals I/(mR2)=2/n2 , what is n3?
Note that n1 and n3 have the same units of speed, and
n2 is unitless. For a ring, n2 = 2; for a disk,
n2 = 4; and for a sphere, n2 = 5.
If you are currently in my class, you can record your grade by entering your name and student ID
number (without the leading zeros) below and clicking on "record grade".

